Difference between revisions of "Introduntion in Korean"
m |
m |
||
| Line 10: | Line 10: | ||
| − | [[Image:RydbergIsing.jpg|right| | + | [[Image:RydbergIsing.jpg|right|600px|none|thumb|그림 1 리드버그 원자 배열로 구현한 아이징 그래프 G=(V,E) : 해밀토니언에서 Ω는 기저원자와 리드버그원자 간의 라비 (Rabi) 진동수, Δ는 레이저 디튜닝(detuning), U는 리드버그원자 간의 상호작용이고, E와 V는 그래프 G의 꼭지점 집합과 간선 집합이다. 빨간색으로 표시된 원자들이 그래프 의 최대독립집합이다.]] |
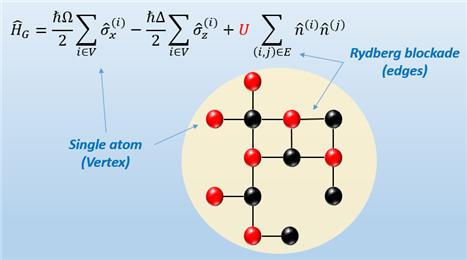
그림 1은 원자 배열을 이용하여 그래프의 최대독립집합을 구하는 실험의 개념도이다. 점으로 표현된 원자는 그래프의 꼭지점에 해당하고, 선으로 표현된 원자간 근거리 상호작용은 그래프의 간선에 해당한다. 이러한 리드버그 원자의 근거리 상호작용은 잘 알려진 아이징(Ising) 해밀토니안으로 표현된다. 실험에서는 해밀토니안을 조절하여, 초기 해밀토니안 H<sub>G</sub>(Ω=0,Δ<0)의 기저상태 원자들을 최종 해밀토니안 H<sub>G</sub>(Ω=0,0<Δ<U)의 기저에너지상태 (빨간점으로 표시된 원자들의 중첩상태)로 바꾸어 그래프 의 최대독립집합을 얻는다. | 그림 1은 원자 배열을 이용하여 그래프의 최대독립집합을 구하는 실험의 개념도이다. 점으로 표현된 원자는 그래프의 꼭지점에 해당하고, 선으로 표현된 원자간 근거리 상호작용은 그래프의 간선에 해당한다. 이러한 리드버그 원자의 근거리 상호작용은 잘 알려진 아이징(Ising) 해밀토니안으로 표현된다. 실험에서는 해밀토니안을 조절하여, 초기 해밀토니안 H<sub>G</sub>(Ω=0,Δ<0)의 기저상태 원자들을 최종 해밀토니안 H<sub>G</sub>(Ω=0,0<Δ<U)의 기저에너지상태 (빨간점으로 표시된 원자들의 중첩상태)로 바꾸어 그래프 의 최대독립집합을 얻는다. | ||
| Line 17: | Line 17: | ||
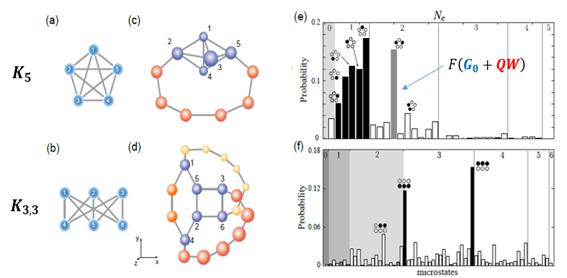
| − | + | [[Image:Kuratowski.jpg|right|600px|none|thumb|그림 2 (a) 쿠라토프스키(Kuratowski) 그래프 K<sub>5</sub>, (b) K<sub>3:3</sub>, (c) 양자선으로 구현한 K<sub>5</sub><sup>QW</sup>, (d) K<sub>3:3</sub><sup>QW</sup>, (e,f) 양자단열실험으로 얻은 K<sub>5</sub><sup>QW</sup>, K<sub>3:3</sub><sup>QW</sup>, 원자배열의 다체기저상태 확률분포[1].]] | |
| − | |||
| − | |||
Revision as of 07:20, 27 July 2022
[뉴스레터 연구동향 (2022.06.21), 양자정보지원센터]
리드버그 원자 배열을 이용한 최대독립집합 NP-완전 문제
(Solving the Maximum Independent Set problem using Rydberg atom arrays)
일정 규모의 양자컴퓨터들이 속속 개발되고 있다. 아직 큐비트의 개수와 구동정밀도가 제한적이어서 범용성을 갖지 못하지만, 특정 계산문제 (특히, 디지털 알고리듬이 비효율적인 문제)에 활용될 수 있을지가 관심을 받는다. 계산문제들은 계산복잡도(computational complexity)에 따라 P(결정 다항)와 NP(비결정적 다항)-문제로 분류되고, NP-문제들은 디지털 컴퓨팅의 알고리듬으로는 효율적으로 계산할 수 없다. 따라서 양자컴퓨터를 이용하여 NP-문제, 특히, 모든 NP-문제에 대한 다항 시간 환원성 (polynomial-time reducibility)을 갖는 NP-완전 (NP-complete) 문제들을 계산할 수 있을지가 주목을 받는다.
최근 KAIST 양자컴퓨팅 연구실은 리드버그 원자 배열을 이용하여, NP-완전문제의 하나인 최대독립집합 (Maximum Independent Set) 계산을 시도하였다[1]. 최대독립집합 문제는 주어진 그래프 (꼭지점과 간선의 집합)에서 간선으로 연결되지 않는 최대 크기의 꼭지점 집합을 구하는 문제이고, 그래프의 크기가 커지면 디지털 컴퓨팅로는 계산량이 지수적으로 증가한다. 리드버그 원자 배열은, 특정 해밀토니언 조건에서, 다체 기저 에너지상태가 최대독립집합의 해와 관련되어 있음이 알려져 있다[2]. 따라서, 우리는 양자단열계산 (quantum adiabatic computing) 실험을 수행하여, 리드버그 원자 배열의 기저 에너지상태를 구하고, 해당 그래프의 최대독립집합과 일치함을 확인하였다.
그림 1은 원자 배열을 이용하여 그래프의 최대독립집합을 구하는 실험의 개념도이다. 점으로 표현된 원자는 그래프의 꼭지점에 해당하고, 선으로 표현된 원자간 근거리 상호작용은 그래프의 간선에 해당한다. 이러한 리드버그 원자의 근거리 상호작용은 잘 알려진 아이징(Ising) 해밀토니안으로 표현된다. 실험에서는 해밀토니안을 조절하여, 초기 해밀토니안 HG(Ω=0,Δ<0)의 기저상태 원자들을 최종 해밀토니안 HG(Ω=0,0<Δ<U)의 기저에너지상태 (빨간점으로 표시된 원자들의 중첩상태)로 바꾸어 그래프 의 최대독립집합을 얻는다.
특히, 우리는 이번 연구에서 리드버그 양자선을 개발하여, 쿠라토프스키(Kuratowski)의 K5와 K3:3 그래프를 실험적으로 구현하였다. 양자선이 없으면, 2차원 또는 3차원 구조의 원자 배열로 구현할 수 있는 그래프의 종류는 제한적이다. 이는 근거리의 원자끼리만 강하게 상호작용하기 때문에, 꼭지점당 간선의 수가 제한되기 때문이다. 이를 해결하기 위하여, 모든 종류의 그래프를 만들기 위해서, 원거리에 배열된 원자를 인위적으로 근거리의 상호작용을 하게 하는 양자선(quantum wire) 개념이 제안되었다[3]. 우리는 리드버그 원자 배열을 이용하여 양자선 개념을 증명하고, 쿠라토프스키 K5와 K3:3 그래프를 실험적으로 구현하였다. 여기서 쿠라토프스키 와 그래프는 모든 비평면 그래프가 반드시 하나 이상 포함하는 부분 그래프이고, 평면 그래프와 K5와 K3:3를 조합하면 원칙적으로 모든 그래프가 구현가능하다.
KAIST가 개발한 리드버그 양자선의 중심 아이디어는, 그림 2에서 보는 바와 같이, 물리적 공간에서 직접 만들 수 없는 K5와 K3:3와 같은 비평면 그래프 G의 최대독립집합을, 양자선으로 연결한 그래프 G0+QW와 양자선을 제외한 그래프 G0의 최대독립집합들을 비교하여 얻을 수 있음을 보인 것이다. 리드버그 양자선의 활용은 2차원 또는 3차원으로 제한되는 원자 배열의 연결구조를 임의의 차원의 원자 배열로 확장할 수 있을 뿐만 아니라, 하나의 꼭지점에 연결되는 간선의 수를 무제한으로 허용하게 되어, 모든 큐비트간 초연결성(N-to-N coupling)을 원칙적으로 가능하게 한다.
리드버그 원자 배열을 이용하는 양자컴퓨팅 연구를 소개하였다. 양자 단열 컴퓨팅을 이용하여, 원자 배열과 양자선으로 프로그램한 그래프의 최대독립집합을 구했다. 최대독립집합을 계산한 위의 양자컴퓨팅 방법은 다른 문제의 계산에 활용될 수 있다. 이유는 하나의 NP-완전 문제를 계산할 수 있으면, 다른 NP-완전문제를 포함한 모든 NP 및 P-문제의 해를 다항 시간 환원 알고리듬으로 구할 수 있기 때문이다. 현재 최대 126개의 원자를 이용하여 일부 그래프의 최대독립집합을 구하였지만, 아직 디지털컴퓨터의 계산한계에 도달하지 못한다. 하지만 실험장치의 개선을 통하여, 수 천개의 원자 배열을 사용하면 양자이점에 도달할 수 있을 것으로 예상되고 있다.
참고문헌: [1] M. Kim, K. Kim, J. Hwang, E.-G. Moon, and J. Ahn, “Rydberg quantum wires for maximum independent set problems with nonplanar and high-degree graphs," Nature Physics, https://www.nature.com/articles/s41567-022-01629-5 (2022). [2] H. Pichler, S.-T. Wang, L. Zhou, S. Choi, and M. D. Lukin, “Quantum optimization for maximum independent set using Rydberg atom arrays,” arXiv:1808.10816 (2018). [3] X. Qiu, P. Zoller, and X. Li, “Programmable quantum annealing architectures with Ising quantum wires,” PRX Quantum 1, 020311 (2020).